ABOUT ME
Download CV
I am Md Abdul Hamid, currently pursuing my PhD in mechanical science and engineering (MechSE) at University of Illinois at Urbana-Champaign (UIUC). I am conducting my research work under the supervision of Prof. Kyle Smith. Our research work focusses on developing transient theories for multi-scale mass transport through porous media with simultaneous advection, diffusion and reaction. Mass transport plays important roles in many geological, biological and engineering processes, including contamination and saltwater encroachment of fresh-water aquifers, distribution of oxygen/carbon-di-oxide gas inside animal/human lungs, drug delivery to organs/brains, packed bed reactors, petroleum recovery in oilrigs, and so on. Despite applicability in other engineering fields, our research work is primarily motivated form flow based electrochemical devices, i.e., redox flow batteries and faradaic desalination cells, where mass transfer is crucial. For such devices transient operation is unavoidable, and deploying conventional theories fails dramatically to predict mass transfer rates under such operations, leading to both safety concerns and inefficient operation. Our goal is to develop a bottom-up transient theory that is not only applicable for transient operations, but also can provide better design guidelines.
I completed my MSc (January 2016) and BSc (February 2013) in mechanical engineering from Bangladesh University of Engineering and Technology (BUET). My MSc and BSc research works were focused on compressible flow past a bi-convex circular arc airfoil in transonic flow regime under the supervision of Prof. A. B. M. Toufique Hasan. Both internal and external compressible flows appear in numerous engineering applications including commercial airplane flight, high-speed gas turbines, compressors and supersonic nozzles. In transonic regime such flows are accompanied by shockwave which increase total drag on the walls, ultimately increasing the operating cost for such devices. Often the intricate interaction between the shockwave and the boundary layer at the solid/fluid boundaries allows the shockwave to fluctuate, a phenomenon called shock buffeting. Buffeting not only causes excessive noise and vibrations, but it also increases the net pressure loss in the system, increasing the operating cost further. The goal of our research work was to numerically investigate the characteristics of shock-boundary layer interaction in transonic flow conditions, and finally to use a proper passive control technique (i.e., cavity incorporation) to decrease shock buffeting and pressure loss in the system.
For details on the theoretical background, techniques, results, and future scopes please visit my research interests page and have a look at my disertations/recent publications on the topic.
NEWS GALLERY
January 15, 2025
Engineers have found a way to eliminate the fluid flow “dead zones” that plague the types of electrodes used for battery-based seawater desalination. The new technique uses a physics-based tapered flow channel design within electrodes that moves fluids quickly and efficiently, potentially requiring less energy than reverse-osmosis techniques currently require...
November 21, 2024
The Smith Group was selected for our Safety Spotlight for the impact they have here at Illinois in conducting safe research. Led by Dr. Kyle Smith, Associate Professor in Mechanical Science & Engineering, the research group is exploring breakthroughs in energy storage, desalination using electrochemical methods to improve access to clean drinking water, and other areas that have significant societal impact...
March 19, 2023
MechSE Associate Professor Kyle Smith and doctoral student Md Abdul Hamid recently published an article in the Journal of Power Sources. Their study, “A bottom-up, multi-scale theory for transient mass transport of redox-active species through porous electrodes beyond the pseudo-steady limit,” demonstrates that conventional theory approaches underpredict the power capacity of flow batteries such as those used in electricity production from renewable energy sources...
November 20, 2019
Redox flow batteries are an emerging technology for electrochemical energy storage that could help enhance the use of power produced by renewable energy resources. These power resources are inherently irregular in their supply, which doesn’t typically align with demand on the power grid. In principle, redox flow batteries can be designed to have an energy-storage capacity that is independent of its power rating...
REDOX FLOW BATEERIEs (RFBs) & TRANSIENT OPERATIONs
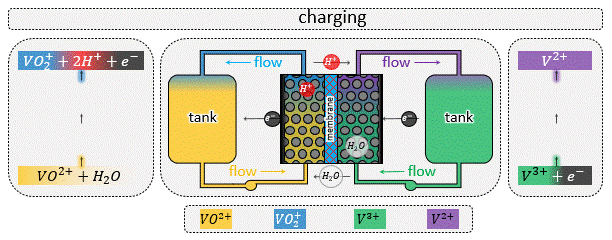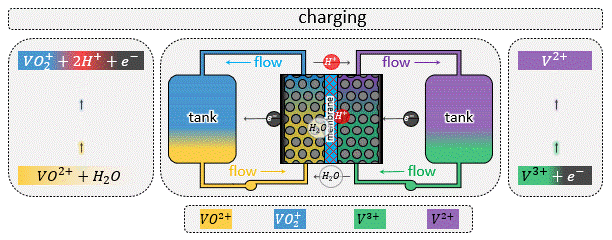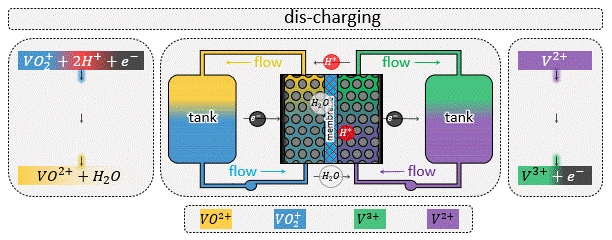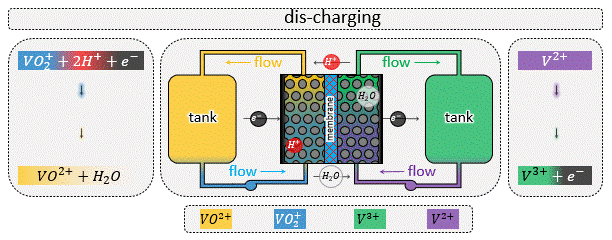
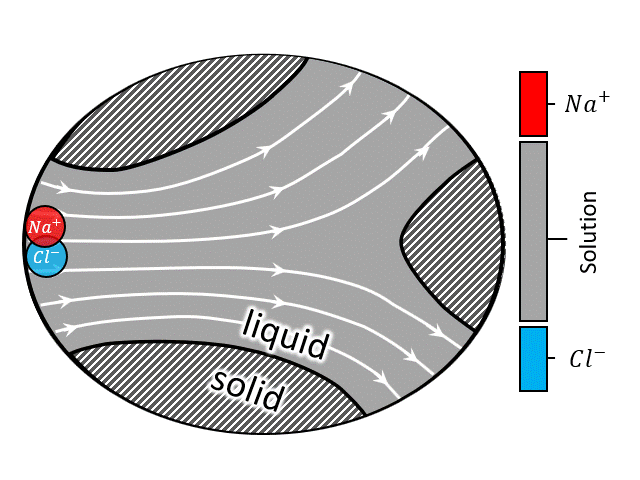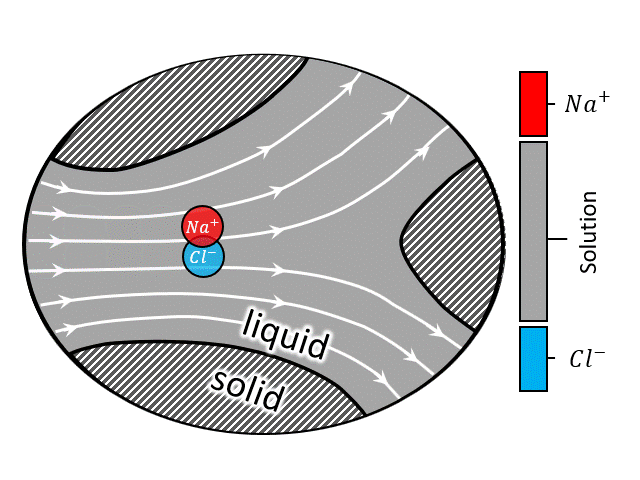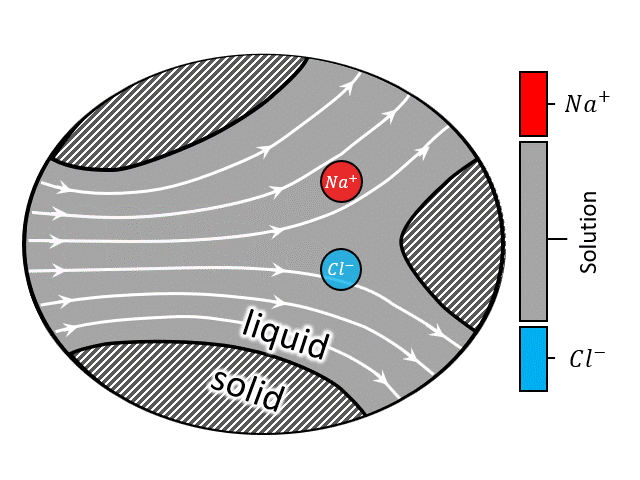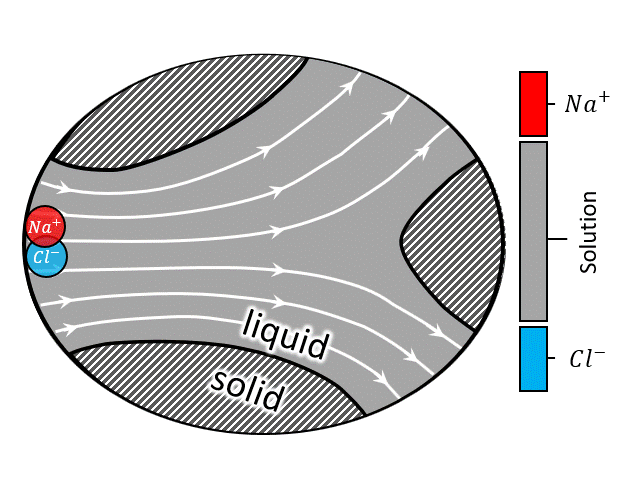
In a flow battery a redox-active liquid electrolyte is circulated through the porous electrodes inside the reactor to and from the tanks, forming two separate closed loops in the two sides of the reactor. See the animation at left (or above) for the fluid flow circuitry between the tanks and reactor. Inside the reactor a heterogenous electrochemical reaction takes place at the solid/solution interface, after which the charged (or discharged) species are carried to the storage tanks.
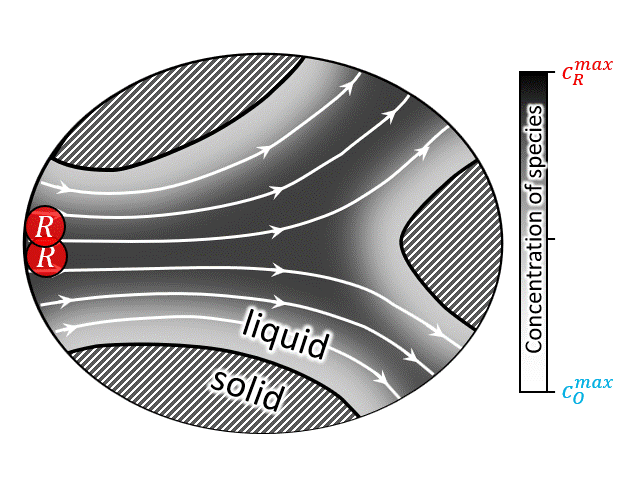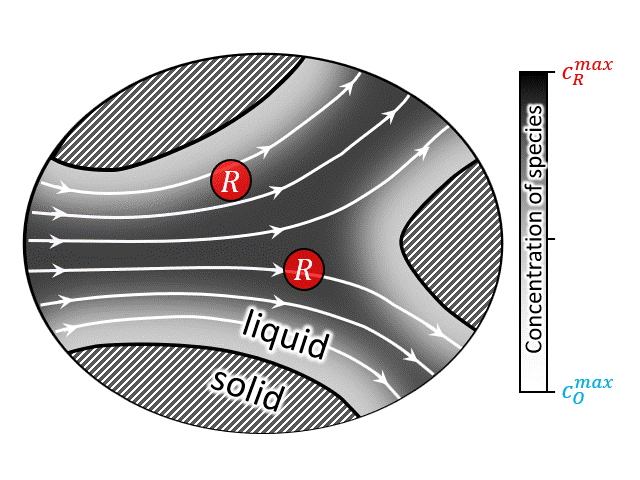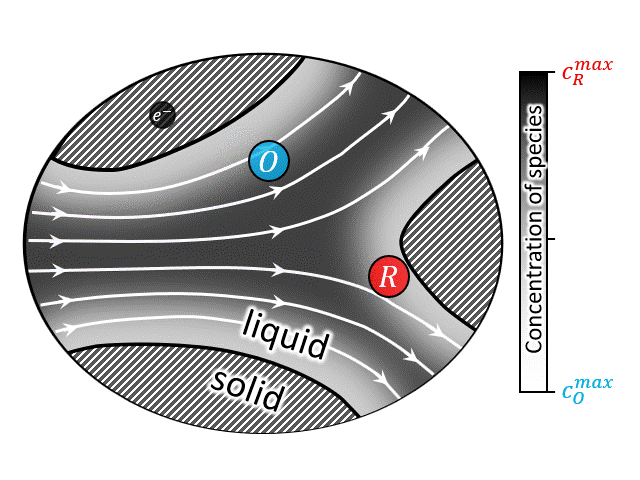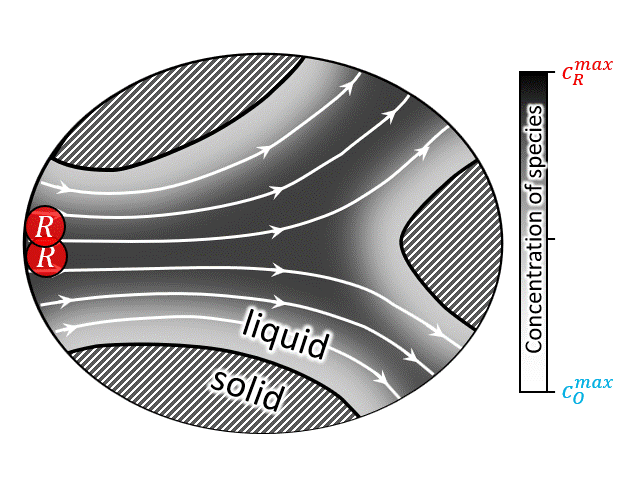
A zoomed in view of the porous electrode is shown in the animation at right (or above), where an electron transfer reaction $$ R \rightarrow O + e^-$$ occurs at the solid/solution interface. In such systems advection by the bulk flow facilitates the supply/evacuation of the reactant/product species to/from the interstitial pores, while diffusion allows the reactants/product species to cross streamlines, enabling them to lose/gain electrons due to an applied current. If the dissolved species are charged, which is most likely the case for conventional flow batteries, along with advection and diffusion, migration plays a role in the rate of solute transport as well. Such devices when assembled with an electric generator to produce power from renewable sources like wind and solar, the total current fluctuates with time due to unavoidable reasons like gusts (∼1 Hz) and daily weather (0.1∼1 mHz). For the sake of comparison, a typical aqueous all-vanadium RFB with carbon-felt electrode has a characteristic frequency range of 0.025∼1 Hz. Therefore, frequency-dependent response of RFBs is likely to play an important role in the efficient utilization of renewable energy sources.
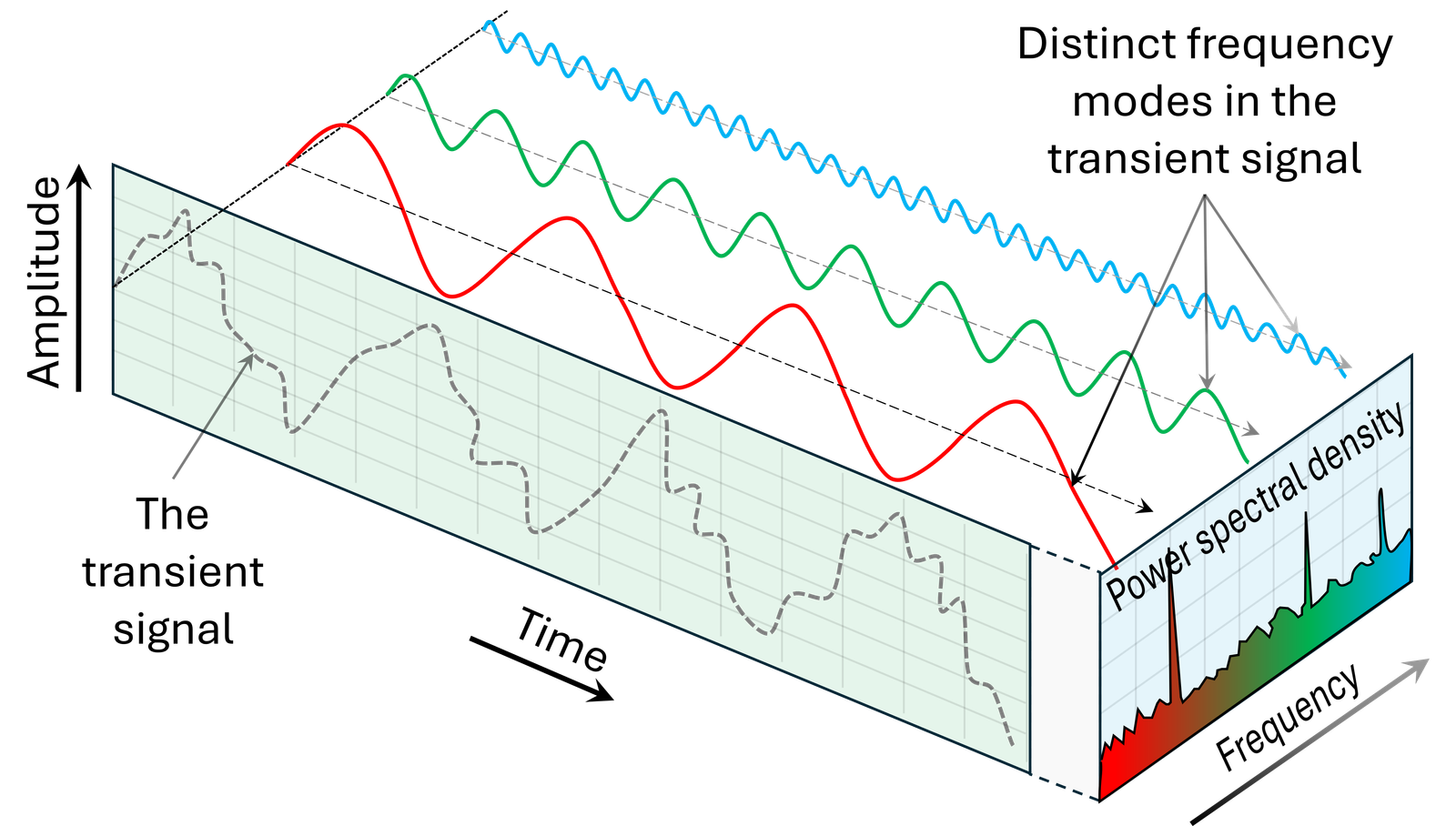
Transient operations: Using Fourier transformation as , where is the transformed form of an arbitrary time dependent parameter and is the angular frequency, any transient signal can be represented by an infinite series of sine/cosine waves of different fundamental frequencies. For better understanding on Fourier transformation the video by 3blue1brown is highly recommended. This concept is widely used in signal processing and schematically shown in the figure at left (or above). Further, from the power spectral density (PSD) the fluctuating transient signal in time domain can be reconstructed using inverse Fourier transform as . The key concept in analyzing systems in frequency domain is to obtain the system response as a complex number, defined by output-input correlations, at discrete frequency modes. An example of such a complex parameter is the complex impedance used to study the transient responses of electrical elements (i.e., resistors, capacitors, and inductors) and their combinations (e.g., RC, RL, RLC branches). For electrochemical systems, Randles circuit model is widely used representation, where electrolyte resistance, double layer capacitance, charge transfer resistance and mass transfer impedance are considered.
KEYWORDS: Transient, Electrolyte, Redox, Flow Battery, Fourier Transform, Complex Number, Complex Impedance, Randles Circuit.
TRANSFER FUNCTIONs (TFs) & TRANSIENT RESPONSE OF SYSTEMs
Since Fourier transform allows us to study transient responses in frequency domain for discrete modes of input frequencies, one can easily define a complex parameter to capture the output-input correlation considering the system as a black box, as shown in the figure below.

In control engineering such black box representations are widely used, where the internal details of the system are inherited by the complex parameter, often referred as transfer function (TF). One example of such a widely used transfer function is the complex impedance of electrical elements (i.e., capacitors, inductors, resistors or any combination of these three) that represents the current-potential relationship under transient operations. Both Bode plots and Nyquist plots are standard ways to graphically represent such frequency domain responses.
The main advantage of such transformation is that it allows to study the transient response of any linear-time-invariant (LTI) system, from which the time domain response for a known input transient can be obtained using convolution between the applied transient and the transfer function. For example, the complex impedance of an electrical element is defined as, $$ \bar Z(\omega) = \frac{\Delta \bar V(\omega)}{\Delta \bar i(\omega)}$$ where, is the change of the transient input current, and is the corresponding change in the transient output voltage. The expression above clearly reveals that the complex impedance (i.e., transfer function) represents the transient response (i.e., ) in frequency domain when the change in the input signal is unity (i.e., ). Further for any non-unitary change in the applied transient current the total response of the system can be obtained as, $$ \Delta V(t) = F^{-1}(\bar Z(\omega) \times \Delta \bar i(\omega)) = Z(t) \otimes \Delta i(t)$$ Here, represents a convolution operation.
Transfer functions for bottom-up multi-scale modeling: It is obvious that before invoking frequency domain representation the governing equations for the underlaying physics need to be transformed, and then the average TFs can be obtained for a representative elementary volume (REV) using averaging techniques like volume/surface averaging. This idea can be applied in a straightforward manner to create a bottom-up multi-scale formulation of a LTI system, where at each point in space an averaged TF is set to capture the underlaying micro-scale physics. These local average transfer functions provide the local responses while keeping the micro-scale details intact, and the overall (upscaled) response is calculated from these local responses following a consistent averaging method. In our work, for the first time, we derived three volume averaged transfer functions from the periodic representation (periodic unit cell) of the porous media. We note that such periodic representation requires additional treatment in the frequency domain approach, which is discussed in our published journals. These transfer functions are equivalent to the "phenomenological transport coefficients" appearing in the Darcy-scale representation of the system using porous electrode theory. The first of these three transfer functions is the spectral Sherwood number, representing effective reaction rate in the up-scale mass transport equation. The second transfer function is a vector representing deviation of the advection rate from the expected value (e. g., average velocity ✕ average concentration) due to the inhomogeneity of local concentration field across the interstitial pores. The third transfer function is an effective diffusion coefficient tensor that accounts for molecular diffusion and hydrodynamic dispersion together.
KEYWORDS: Black Box Modeling, Transfer Function, Multi-Scale-Modeling, Bottom-Up, Bode-Plot, Nyquist Plot, Convolution, Porous Electrode Theory.