← BACK TO HOME
"Research is what I'm doing when I don't know what I'm doing"
— Wernher von Braun (German-American Aerospace Engineer)
Sunrise @ Mitre Peak, New Zealand. © Photo credit -Steffen Walther
Hamid |
HOME UIUC BUET GOOGLE GMAIL LinkedIn
THESIS DISERTATIONs
PATENT APPLICATIONs
JOURNAL PUBLICATIONs
CONFERENCE PRESENTATIONs

RESEARCH INTERESTs

  • Transport in porous media:
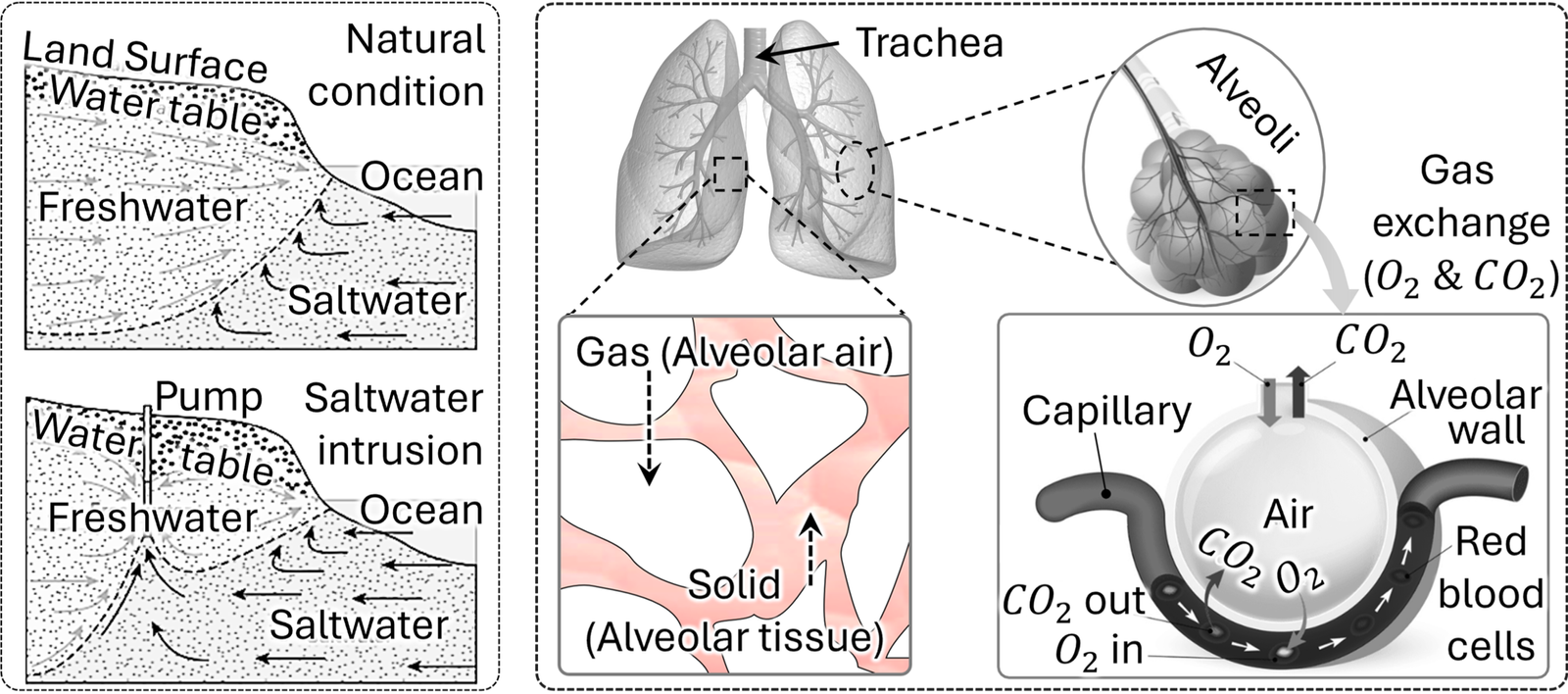
RFB half cell

Assume a porous medium where the two sides are filled with fluids with different solute concentrations and the sides are separated using a removable barrier. When the barrier is removed the solutions on both sides are allowed to mix freely over time. The animation at right (or above) shows the time evolution of the average concentration inside the porous medium. It is evident that the length of the mixing zone in such system increases with time due to the transport of dissolved species which is greatly affected by three types of parameters associated, (a) geometry of the medium- e. g., porosity, tortuosity, (b) material properties- e. g., diffusivity of dissolved species and (c) imposed conditions- e. g., flow rate of the bulk solution (if the fluids are moving). Further, presence of reaction at the solid/solution interface causes non-uniform concentration distribution across interstitial pores, affecting the net flowrate of the dissolved solutes. Both reactive (with reactive interfaces) and inactive (without reactive interfaces) solute transport are important in many natural processes, including geological and biological systems. Some of the examples are, ground water contamination, saltwater intrusion in costal aquifers, air flow in animal lungs, drug delivery systems into brains/tissues etc. The geological processes mentioned earlier pose a worldwide threat toward freshwater scarcity, whose remedy depends on accurate prediction of dissolved solute/salt transport through porous soil, rocks, gravels, and sands [1–4] . Meanwhile air flow patterns and gas (Oxygen and Carbon-di-Oxide) exchange rates within human lungs [5–8], and drug delivery systems [9–11] into brains/tissues to/from blood stream [5–8] are often studied using porous media models. Brief examples are shown in the figure below (sources of partial images can be found here).

RFB half cell

Inactive and reactive transport also plays an important role in technologies targeting long run environmental solutions, like underground sequestration of Carbon-di-Oxide [12,13] and corrosion prevention of underground radioactive waste repositories [14,15]. Many engineering applications depend on similar physical processes where dissolved solute species are transported through a porous media, with or without heterogeneous reactions occurring at the solid/solution interface. Such applications include, but are not limited to, underground oil recovery systems using miscible displacement process [16,17], catalytic converters [18,19] and flame stabilization using a porous media reformer [20,21]. Further heat and mass transfer analogy can be applied to study the heat transfer through porous metallic structures since the fundamental physics of diffusive mass transport and heat conduction are similar [22,23].

In flow based electrochemical devices, like redox flow batteries and electrochemical desalination cells, reactive transport plays a crucial role. Here a liquid electrolytic solution containing dissolved active ionic species is pumped through reactors containing porous electrodes. While being transported through the porous reactor, the active solutes undergo a heterogeneous redox reaction at the solid/solution interface by losing/gaining electron(s) causing an electric current. Though the solution phase ion transport between these two devices is similar, differences arise regarding how the ions are stored following the electrochemical reaction. In capacitive deionization the ions are stored inside the solid phase via an insertion mechanism (i.e., intercalation), while in RFBs the species are carried to a tank by the bulk flow where they are stored. In both cases the solution phase ionic transport dictates the rate capabilities, provided that the reaction kinetics is comparatively fast.

RFB half cell

SCOPE: In this context, literature still lacks a rigorous theory regarding the question “how to obtain the macro-scale transport coefficients for mass transfer rates through porous media in the presence of advection, diffusion and reaction form a representative unit volume?”. Up-to-date, only two different foundational theoretical approaches are found in literatures: Brenners method of moment [23–28], and Whitakers method of volume averaging [29–34]. Both methods face challenges in elucidating the structure of the phenomenological coefficients appearing in the macro-scale transport equations and are applicable only in the long-time limit, when the characteristics time scale of the transient is large compared to the diffusion time scale. The key concept is schematically shown in the figure at right (or above). (See references)

  • Reactive transport in flow batteries:
RFB half cell

According to National Renewable Energy Laboratory report 2019, renewable energy sources are projected to comprise approximately 60% of US electricity generation by 2050, with wind and solar power contributing approximately 2000 and 1000 TW-h respectively [35]. Large-scale energy-storage devices are a must have component in these power plants to overcome the mismatch between electricity demand and intermittent supply arising from the stochastic nature of wind and the diurnal cycle of solar insolation [36]. Among other technologies, redox flow battery (RFB) has drawn special attention due to its ability to independently scale power and energy-storage capacity. A brief video on the working principle of RFBs can be found here, which shows that such devices operate by circulating a redox-active liquid electrolyte through the electrodes to and from tanks, forming a closed loop. The two sides of such devices are separated by a membrane that allows protons (and water molecules) to be transferred across it, while blocks active ion crossover. Thus, often it is convenient to look at the half-cell operation of such devices as shown in the animation at right (or above). The animation shows an electrochemical reaction where a reduced ion R (reactant) is being oxidized to O (product) by losing an electron. $$ R \rightarrow O + e^-$$ After the reaction is complete the oxidized species O is then carried out into the tank following the electron transfer reaction.

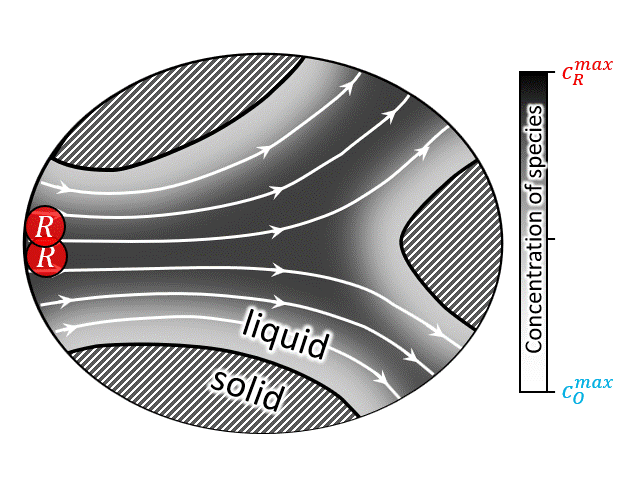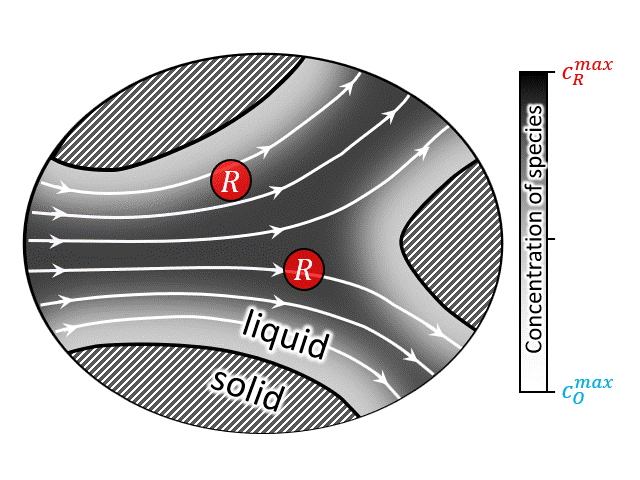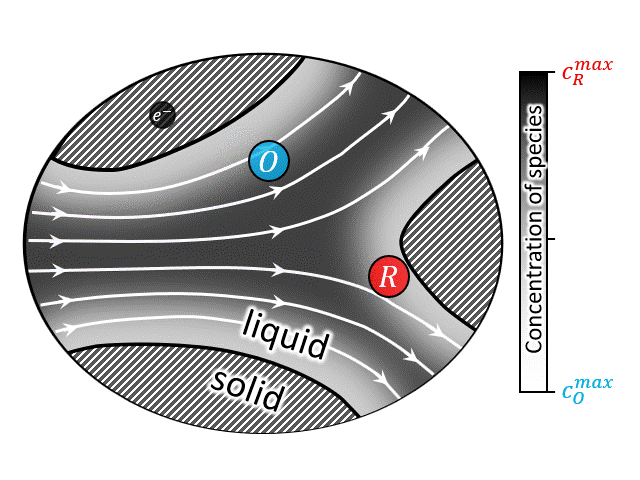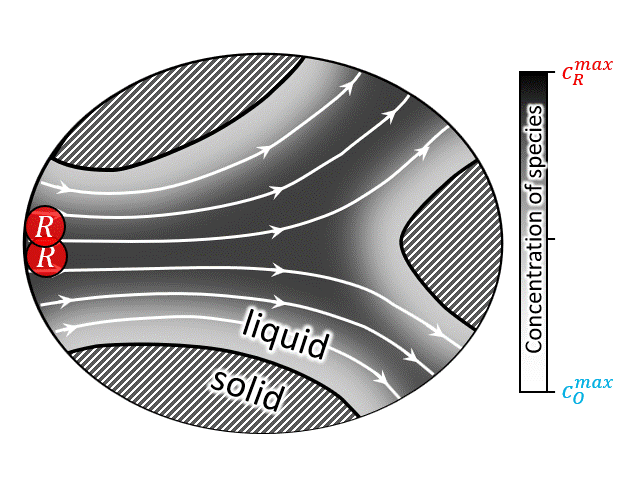
RFB half cell

A closed-up view of the pore-scale transport physics is also shown in the animation at left (or above). It is evident that all modes of mass transport (i.e., diffusion, advection, and migration) contribute to the total flux of the species. However, it can be shown that under certain conditions (i.e., enough supporting salt) the contribution of electromigration is negligible and the pore-scale mass transport equation can be written as an unsteady advection-diffusion equation. It should be noted that the heterogenous electrochemical rection only occurs at the solid/solution interfaces (i.e., solid/solution boundaries), thus this physics only appears in the boundary conditions. These boundary conditions represent the current-potential relationship at the interface which is non-linear in nature. Due to nonlinearity, as well as complexity of the porous geometry, an analytical solution to the transient advection diffusion equation is nearly impossible. A numerical solution for such a large macroscale domain (order of meters) with pore-scale resolution (order of micro-meters), is prohibitively expensive. To overcome this issue upscaling, i.e., volume averaging, is often used to predict/design such devices [29,30,32,34,37,38]. While upscaling, major challenge arises regarding the preservation of the underlaying pore-scale physics while calculating the upscale transport coefficients.

To obtain the upscaled transport coefficients we used a rigorous volume averaging approach while appropriate measures are deployed to tackle the local discontinuity in the pore-scale concentration field. The mathematical formulation is derived in the frequency domain for a periodic unit that is representative of the entire electrode. An ad-hoc ansatz is utilized by taking the first two terms (i.e., linear approximation) in the Taylor series expansion of the local average concentration, which yields two closure problems for the two coefficients appearing in the invoked ansatz.

RFB_Scope.png

SCOPE: The figure at right (or above) shows the physical limit on the applied current due to mass transport limitation in electrochemical devices, which is often referred as the limiting current. Operation of RFBs close to this limit causes excessive concentration polarization (potential loss corresponding to the reduction of reactant concentration near electrode/electrolyte interface). However conventional theories use time invariant Sherwood number (i.e., non-dimensional mass transfer coefficient) to predict the limiting current and associated concentration polarization. Limiting current from time invariant Sherwood number (LCfTISN) can underpredict the devices rate capability, as it over predicts the concentration polarization under transient operation. It has been shown that such devices can operate with applied current higher than the LCfTISN when the transient time scale is must shorter [39,40]. This idea can be explored both experimentally and numerically, which can provide a means to increase the utilization of charge capacity of an existing RFB operated under transient conditions with proper safety understanding. (See references)

  • Ion transport in desalination electrodes:
RFB half cell

The unavoidable demand/utility of fresh groundwater is increasing day-by-day worldwide. For example, groundwater withdrawals from Atlantic and Pacific coastal regions following the year 2000 are more than 600 cubic-meter-per-second (~14 billion gallons per day) according to the US Geological Survey 2004[41]. Aside from contamination, the proximity of coastal aquifers to saltwater creates unique problems as the salt water slowly gets mixed with the fresh water increasing its salinity. The figure at right (or above) shows a world map of saltwater intrusion into the coastal regions [42]. With increasing industrialization and world population, the remedy to the scarcity of fresh water requires more advanced and efficient technologies. The current state-of-the-art technology, i.e., reverse osmosis, is considered the most efficient technology for seawater (salinity ~35g/L) desalination. In this process, fresh water is produced by forcing the seawater through a semipermeable membrane against the osmotic pressure. Though this technique can produce freshwater at an average cost of $0.1 per cubic meter (levelized cost) [43], its energy efficiency goes down for low concentration feed (salinity ~5g/L) [44]. Moreover, the nonselective nature of this process removes all the dissolved ions from the water voiding the nutrition value for irrigation/drinking, which often accumulates additional cost in adding the necessary nutrients before consumption by plants/animals.

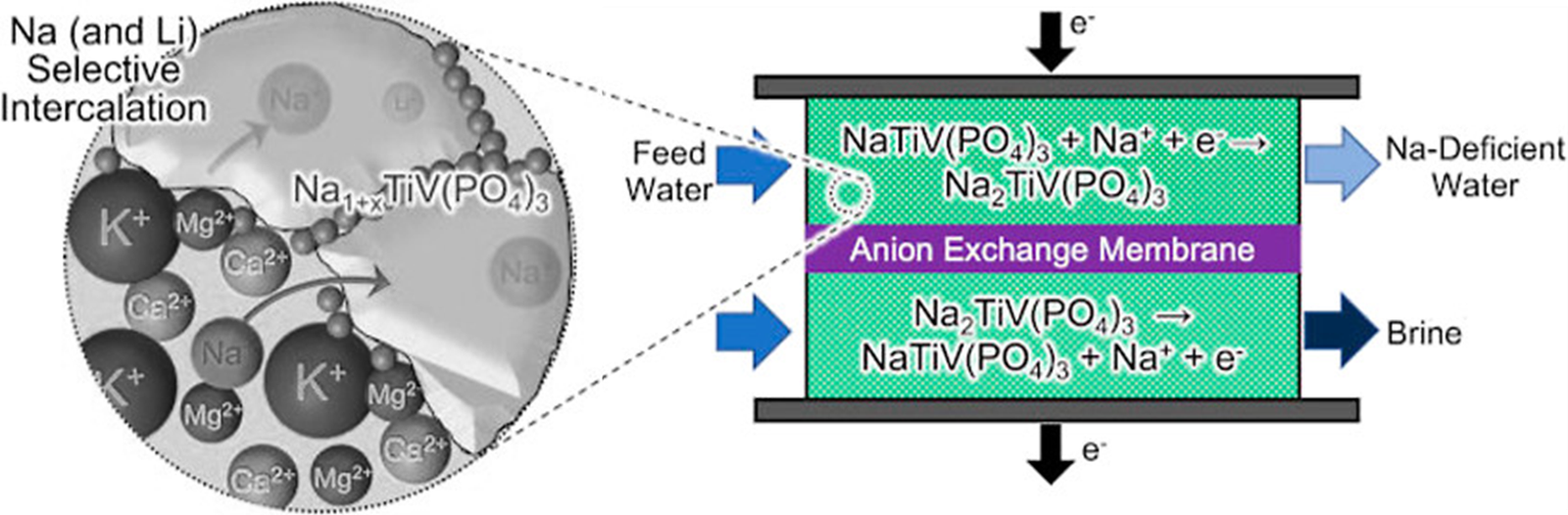
RFB half cell

Though electrodialysis can provide selective deionization, it includes exhaustive use of prohibitively expensive ion exchange membranes, increasing the water purification cost up to ~$1.5 per cubic meter from seawater [45]. Under all these circumstances, Faradaic deionization revealed itself as a potential candidate for efficient and selective deionization of saltwater. This technology uses porous electrodes as a host compound for the target ion which are separated by a cation exchange membrane. The host compound provides necessary space in its lattice sites for the target ion to sit. This ion insertion process is identical to the process of lithiation in Li-ion batteries, known as intercalation.

The figure above schematically shows the working principle of a faradaic desalination cell [46], where the electrodes are made of Sodium Superionic Conductor (NASICON), which shows substantial selectivity toward sodium ions. Other candidates for faradaic deionization electrodes are metal organic frameworks (i.e., Prussian Blue analogues) [47,48]. In such devices, when the electrode on one side is being intercalated, the opposite side electrode is being deintercalated. Thus, an uninterrupted-continuous stream of purified water can be obtained using current reversal and valve switching [49,50].

RFB_Scope.png

SCOPE: Concentration polarization reduces the utilization of capacitive electrodes during Faradaic desalination [51,52], as it causes local depletion of reactant inside the electrode. This can be overcome by facilitating ion transport (i.e., increasing the feed flowrate) through the pores of the flow-through and flow-by electrodes, which increases the pumping power as well. Another idea is to engrave microchannels (i.e., interdigitated, serpentine patterns as shown in the figure at right or above) on the porous electrode to reduce the flow path, which ultimately reduces the pumping cost even at high flow rates. This technique is widely used and tested to be an effective means in reducing the concentration polarization. An up-scale model using transient mass transport theory (i.e., effective up-scaled transport coefficients) can be used to study and analyze the performance of micro-channel engraved electrodes. (See references)

  • Transonic flow around an airfoil:
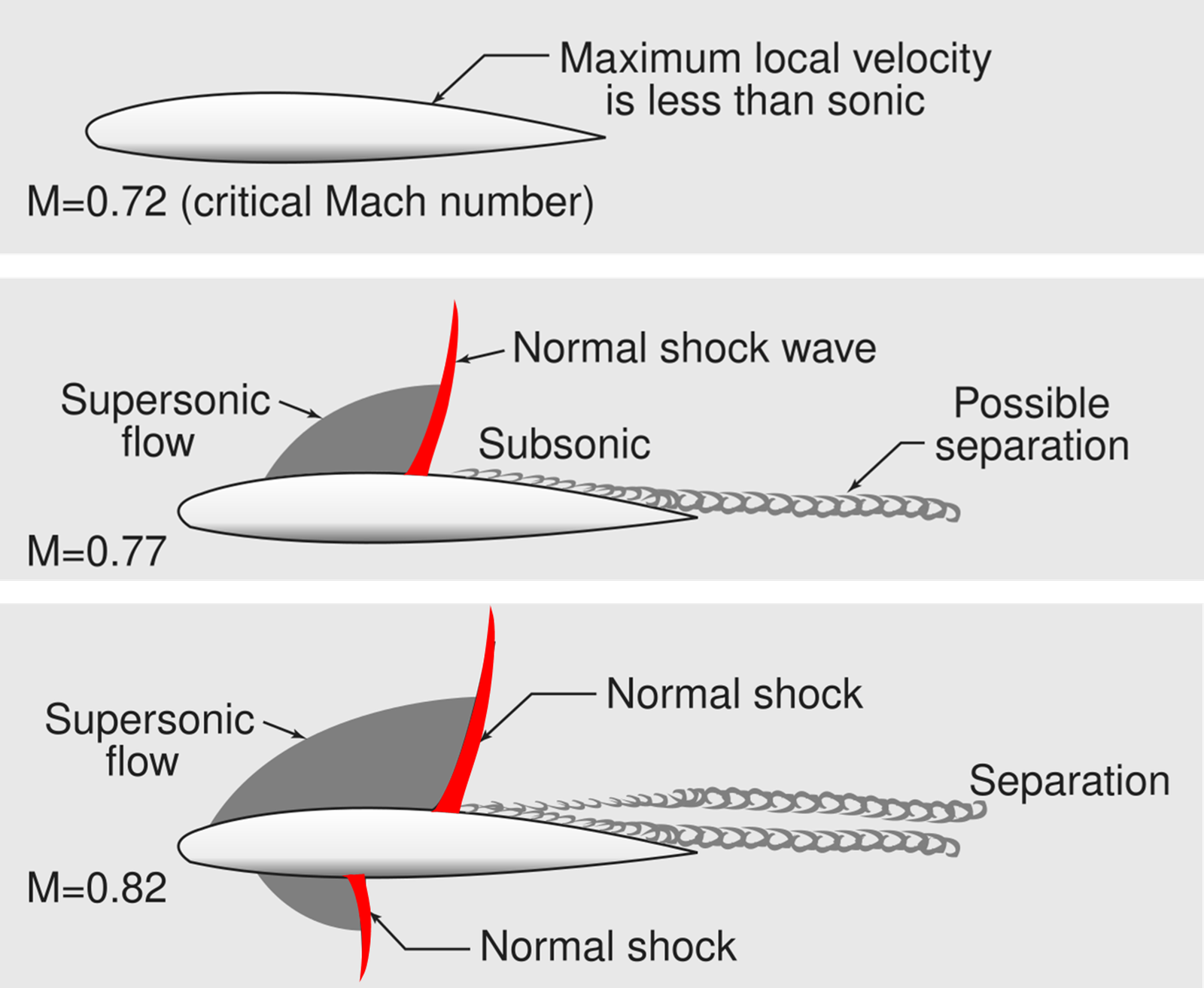
Transonic flow regions

A transonic flow is characterized as a compressible flow where both subsonic and supersonic flow regions coexist, which often forms a thin layer of flowing fluid between these two regions. Across this thin layer of fluid, local properties (e.g., density, pressure and temperature) change drastically, which is commonly known as a shockwave. Such phenomenon is schematically shown in the figure at right (or above). Formation of such shockwaves causes additional drag on the airfoil known as wave drag, ultimately increasing the fuel consumption rate during commercial aircraft flights [51]. Aside from external-high-speed-flow applications, similar phenomenon is observed in internal-high-speed-flow applications, such as gas turbines, compressors and supersonic nozzles [52–55]. A complete remedy of wave drag in transonic flows is impossible as the shockwave is necessary to accommodate the drastic pressure difference between two sides of the airfoil.

Shock Buffeting

Under specific conditions the shockwave starts to fluctuate with time as shown in the animation at left (or above), a phenomenon known as shock buffeting. Buffeting not only causes additional drag on the airfoil, but it is also associated with high amplitude noise and vibrations. B. H. K. Lee proposed a self-sustained feedback mechanism (see figure below) to explain shock buffeting [56,57], opening new insights for shock controlling techniques.

Feed-back Mechanism

Both active and passive control techniques are proposed in numerous literatures [58]. Active techniques require external power supply, which comes with an additional operating cost. Such techniques include suction/blowing of the boundary layers in front/back of the shock-foot, heating/cooling of the airfoil surface etc. Passive techniques do not require additional power, thus are economically more favorable. Such techniques often dels with airfoil geometry modifications, like incorporating bumps, cavities, flaps (Gurney) etc. During my MSc thesis work, we numerically studied the effect of cavity geometry and location on the shock wave strength. Raynolds-averaged Navier-Stoke (RANS) equation is solved, along with mass and energy equation, for two-dimensional isothermal flow over a biconvex-circular arc airfoil. The obtained result shows that both open and perforated cavities can reduce the pressure fluctuations and integrated total pressure loss (ITPL). Note that the pressure fluctuations at the airfoil surface is the primary cause for buffeting, and ITPL is directly related to the total energy consumption. Though open cavities showed significant reduction in buffeting (~75% reduction) and ITPL (~8% reduction) it increases shock strength in the far field. Higher shock strength at the far field may have detrimental consequences for internal flows through compressor/turbine rotor-blades, as shockwaves from adjacent blades can interact with each other. On the other hand, perforated cavities do not show significant change in the shock strength in the far field, but they can reduce shock buffeting up to 70% and total pressure loss up to ~8%, which is very similar to the open cavities. Thus, perforated cavities are more suitable as shock control techniques over open cavities in internal flow applications.

Feed-back Mechanism

SCOPE: For internal transonic flows through rotor blades of gas turbines and compressors, the interaction between two shockwaves generated on the surface of two adjacent airfoils needs to be studied further. The figure at left (or above) shows such interacting shockwaves, where the local pressure field can be obtained by superimposing the two pressure fields caused by the individual shockwaves (generated on two separate yet adjacent airfoils). There could be a scope to use such interactions to achieve power benefits. The goal here is to superimpose the two fluctuating shockwaves with ~180-degree phase difference so that they weaken each other without any external power requirements. For specified airfoil shape/size, this can be achieved through careful designs of blade angles, blade spacing and blade offsets as shown in the figure left/above.(See references)

References
  1. M. Shamsudduha, G. Joseph, S. S. Haque, M. R. Khan, A. Zahid, and K. M. U. Ahmed, “Multi-hazard Groundwater Risks to Water Supply from Shallow Depths: Challenges to Achieving the Sustainable Development Goals in Bangladesh,” Expo Health, vol. 12, no. 4, 2020, doi: 10.1007/s12403-019-00325-9.
  2. N. N. Alfarrah and K. Walraevens, “Groundwater overexploitation and seawater intrusion in coastal areas of arid and semi-arid regions,” Water (Switzerland), vol. 10, no. 2, 2018, doi: 10.3390/w10020143.

THESIS DISERTATIONs

PATENT APPLICATIONs

  • Kyle C. Smith, Md Habibur Rahman, Irwin C. Loud, Vu Q. Do, Md Abdul Hamid and Colby Warden, Tapered, interdigitated channels for uniform, low-pressure flow through porous electrodes for desalination and beyond, US Provisional Patent Application 63/743995, 2025.